https://arxiv.org/abs/2102.09844
Introduction
データに対して、対称性を利用して(CNNによって画像が回転してもetcでとらえられるように、GNNでグラフの点を入れる順番が前後しても同じもの扱いされるように)
多くの問題では、データが3次元空間での平行移動や回転に対して対称性を持つ(分子構造や化学特性予測、物理シミュレーション、3D点群データの認識)
これらはユークリッド群の上であるといえる。
この等価性を保つには、CNNなどの手法があるがそれだけでは不十分。先行研究では中間表現に対してメスを入れてたが、その中間表現を計算するのに計算コストが高い。
この研究では、ユークリッド群にまで拡張した新しいアーキテクチャを提案した。
Background
同変性(Equivariance)
- ある抽象群について考える。同変性を持つ関数とは以下のようなもの。
- 入力空間についての変換と、出力空間について、変換が存在する。
- 以下のように、してからでするのと、した結果になったのをでまた変換しても、同じ値となる。
- 具体例として、平行移動同変性がある。だけ入力を平行移動させると、だけ出力を平行移動させないといけないという条件を、は満たさないといけない。
- 機械学習でよく考えられる、同変性には3つある。
- 平行移動同変性。平行移動させても同じ。
- 回転同変性。という直交行列で回転を実現。回転させても同じ。
- 順列同変性。順列を変えても同じ。入力についての順列について。
Graph Neural Network
GNNは順列同変性を持つ、グラフについてのDNNである。
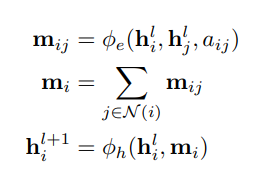
このように、隣接した頂点と、その辺にある情報を受け取り、それを集計することでとなり、最終的に次の自分の頂点の要素は今の要素と周辺の情報によって作られる。は一般的にMLPで実現。
同変性を持つGNN
Equivariant Graph Neural Network(EGNN)
入力として、以下のものを受け取る。
- は各ノードの埋め込みベクトル。
- は各ノードの座標埋め込みベクトル。
- はグラフの辺の情報。辺は引き続き重みもある。
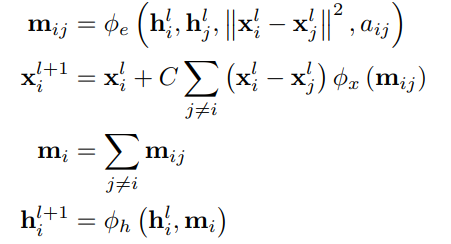
- 辺の埋め込みに加えて、2つの座標埋め込みでユークリッド距離を計算し、それを辺の埋め込みの代わりにする。(つまりの入力は増える)
- 周辺ノードからの情報の集約、自分自身の更新はそのまま。
- 座標の更新は、新たなMLPのを用いて、そこには辺の更新情報埋め込みを入れる。そして、今の点の間の座標埋め込みの差を乗じて、最後に合算する。
- これが毎回の更新の差分。
同変性の分析
GNN自身は順序同変性があるので、平行移動や回転の同変性を持つ必要がある。
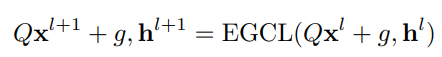
直感的には、
- は距離の二乗距離がある。これは、平行移動と回転に対して不変であるので、も不変性を保持する。
- の更新について、差分の更新も平行移動と回転について不変である。
ベクトル型の表現への拡張
速度の漸化式も、距離埋め込みのような計算と同じ式で応用できるらしい。
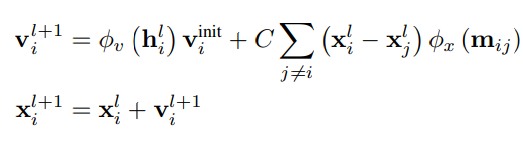
辺の推論
辺の連結情報がないと完全グラフと仮定するしかないが、大規模の点群では数が多すぎる。
その時、近隣ノードの集合を定義してそこだけで辺を張る。
それか、辺を推定する。
